My most recent story, Terminal Proof, is what I like to call horror fiction for nerds. For the rest of us, here is why the story is scary.
Terminal Proof, explained
In the horror fiction for nerds story, our poor student has stumbled across a proof that he is not real. The story, being very short, does not hold your hand with the maths or the computer science beyond reminding you that they exist.
Signed byte overflows
Very quickly I am going to explain a signed byte overflow. This is the same as a binary overflow but with signed bytes.
With signed bytes the most significant bit indicates sign.
00000001 - one 10000001 - negative one (signed) or 129 (unsigned)
You can probably already see what happens when we add two to a large binary number, say 127.
01111111 + 00000010 = 10000001
Which, with a signed byte, is negative one rather than 129. This is the signed byte overflow. In computer science that are a number of ways around this problem but they mostly end up with “don’t work with numbers that are too big”.
The character then goes on to argue that the Riemann zeta function shows a signed binary overflow error with reality. Let’s look at that because this truly is what makes the horror fiction for nerds work.
Proof of the sum of all natural numbers is 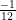 .
.
The answer for the sum of all natural numbers is a product of something called the Riemann zeta function using something called analytic continuation. We can conclude that this character is a maths or physics student of some kind. Here is the mathematical explanation of how you get to . This maths could be seen as horror fiction for nerds until you start to see how compelling the proof actually is.
Now what?
Following the logic that he is seeing a signed binary overflow in “the real world”, the character turns to the Turing Test. The idea of the test is to see if a computer can fool a human into thinking it is another human. The questions that the character asks are example questions from such a test.
The character is panicked and thus no longer thinking clearly and he tries two of the classic questions imagined by Turning.
With the original questions, the challenge for the computer is to demonstrate empathy for the role of the female and to demonstrate as well a characteristic aesthetic sensibility. Instead, with the hair question, the character first gets a plausible, if a rather unlikely, reply but from a professor. Who knows maybe professors are quirky enough and might be the type to say such things.
He then switches to a poetry question. The poem he uses is Sonnet 18 by William Shakespeare. Here he sees the professor not appreciating that there might be an aesthetic quality in the poem and so concludes that his worst fears are real. After all, a human should know that no one would want to be compared to a winter’s day, right?
Horror fiction for nerds
What I rather hope will keep you up at night is that the exchange could happen with a professor (who has time to entertain a student suffering an existential crisis) and that the maths and computer science are all 100% real. In other words out world may, in fact, be a computer simulation.
The proof of this having been laid out and accepted results in termination of the character. Making his proof a terminal proof. Thus, the horror fiction for nerds hits home with the implication that this might be our truth but admitting it could be terminal. Try not to think about the fact that there is no proof that we are not computer simulations.
Don’t panic.

